Example 20

Case-Study XX: Limits of Acceptability: Soil Temperature Modeling

In the manifesto for the equifinality thesis, Beven (2006) suggested that a more rigorous approach to model evaluation would involve the use of limits of acceptability for each individual observation against which model simulated values are compared. Within this framework, behavioral models are defined as those that satisfy the limits of acceptability for each calibration observation. The twentieth case study briefly describes the application of DREAM to sampling the behavioral parameter space that satisfies the limits of acceptability of each observation.

We use a simple illustrative example involving modeling of the soil temperature, T, in degrees Celsius using the following analytic equation

where z (cm) is the depth in the soil profile (positive downward), t (hour) denotes time, T0 (oC) is the annual average temperature at the soil surface, A0 (oC) is the amplitude of the temperature fluctuation, 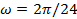 (hour-1) signifies the angular frequency,  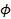(hour) is a phase constant, and z0 (cm) denotes the characteristic damping depth.

A synthetic record of hourly soil temperature observations at 5, 10, and 15 cm depth is used to illustrate the application of DREAM to informal Bayesian inference using a limits of acceptability approach. This data set was created by solving Equation (20.01) numerically for a 2-day period using T0=20oC, A0=5oC, ϕ=8 hr and z0=20 cm. The hourly data was subsequently perturbed with a normally distributed error of 0.5 oC and stored as the n-vector 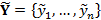.  The limits of acceptability were set to be equal to two degrees Celsius for each of the n = 144 temperature observations at three depths. The four model parameters are listed in Table 20.01 and stored in the d-vector 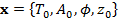. We now determine the behavioral parameter space from the observed temperature data using the following pseudo-type likelihood

where 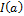is an indicator function that returns one if the condition a is satisfied and zero otherwise. A behavioral solution will satisfy the limits of acceptability of each temperature observation in the soil and thus receive a score of n.

Table 20.01: Parameters of the soil temperature model in Equation (20.01)

We now explore the behavioral solution space (might not exist!) with DREAM. We assume a noninformative (uniform) prior distribution for each of the four parameters using the ranges listed in Table 20.01. A total of N = 10 different Markov chains are used with DREAM. Their initial position is drawn randomly from the multivariate uniform prior using Latin hypercube sampling. Default values of the algorithmic variables are used.

Note, in the present study each observation is assumed to have the same limits of acceptability. DERAM allows the use of a different limits of acceptability for each individual observation. This will be demonstrated explicitly in the next case study involving characterization of the spatial variability of soil moisture in a field plot using numerical solution of Richards’ equation.

Implementation of plugin functions

The complete source code can be found in DREAM SDK - Examples\D3\Drm_Example20\Plugin\Src_Cpp