Example 21

Case-Study XXI: Limits of Acceptability: HYDRUS-1D model

This twenty-first case study considers the application of the limits of acceptability framework to the modeling of the spatial distribution of soil moisture in a field plot. Beven (2006) has suggested that this framework constitutes a more rigorous approach to model evaluation. Within this framework, behavioral models are defined as those that satisfy the limits of acceptability for each calibration observation. The twentieth case study briefly describes the application of DREAM to sampling the behavioral parameter space that satisfies the limits of acceptability of each observation.

We use soil moisture data from an agricultural field near Jülich, Germany. This data was measured over a period of 210-days using Time Domain Reflectometry (TDR) probes installed at 6 cm deep and at 61 different locations in a 50 × 50 m plot. The TDR data were analysed using the algorithm described in Heimovaara et al. (1990) and the measured apparent dielectric permittivities were converted to soil moisture contents using the empirical relationship of Topp (1980). Measurements were taken on 29 days between 19 March and 14 October 2009, comprising a measurement campaign of 210 days. The observed soil moisture data at the 61 different locations were averaged to obtain a single mean time series of water content for the experimental plot. We store this data in the n-vector .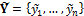

The HYDRUS-1D model of Simunek et al. (2008) was used to simulate variably saturated water flow in the agricultural field. This model solves Richards' equation for given (measured) initial and boundary conditions

where 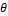(cm3/cm3) denotes moisture content, t (days) denotes time, z (cm) is the vertical (depth) coordinate, h (cm) signifies the pressure head, and K(h) (cm day-1) is the unsaturated soil hydraulic conductivity. Observations of daily precipitation and potential evapotranspiration were used to define the upper boundary condition of the field plot. Precipitation and other meteorological variables were recorded at a meteorological station located 100 m west of the measurement site. A schematic overview of the model setup appears in Figure 7.01. Details of the site, soil properties, experimental design and measurements are given by Scharnagl et al. (2011) and interested readers are referred to this publication for further details.

We have used a similar setup as in case study VII and interested readers are referred to this study for further details. The MVG parameters 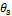(cm3/cm3), 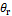(cm3/cm3), 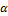(cm-1), n (-) and 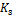(cm day-1) are subject to inference. In the absence of direct measurements, a constant head lower boundary condition, 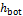(cm) was assumed. The value of 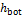is assumed to be temporally invariant and subject to inference with DREAM.

Table 21.01 lists the parameters of the HYDRUS-1D model and their prior ranges. These 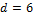parameters are now subject to inference using the mean soil moisture values at the field plot and their associated limits of acceptability.

Table 21.01: HYDRUS-1D model parameters and their prior uncertainty ranges

We now determine the behavioral parameter space from the observed temperature data using the following pseudo-type likelihood

where 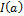is an indicator function that returns one if the condition a is satisfied and zero otherwise. A behavioral solution will satisfy the limits of acceptability of each temperature observation in the soil and thus receive a score of n.

We now explore the behavioral solution space (might not exist!) with DREAM by using the fitness function of Equation (21.02). We assume a uniform prior distribution with ranges of the parameters listed in Table 21.01. We run a total of N = 8 different Markov chains whose initial state is drawn randomly from the uniform prior distribution using Latin hypercube sampling. Default values of the algorithmic variables are used.

Implementation of plugin functions

The complete source code can be found in DREAM SDK - Examples\D3\Drm_Example21\Plugin\Src_Cpp