Case-Study XV: Approximate Bayesian inference using 10 bivariate normal distributions
In this fifteenth study we illustrate the use of Approximate Bayesian Computation (ABC) by application to a target distribution consisting of ten bivariate normal distributions. We first sample randomly ten times the mean, 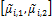 , of a bivariate normal distribution,
, of a bivariate normal distribution, 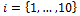 by drawing randomly from a two-dimensional uniform prior distribution,
by drawing randomly from a two-dimensional uniform prior distribution, 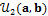 with
with 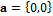 and
and 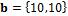 or
or 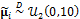 , where the tilde symbol ‟
, where the tilde symbol ‟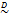 ” means ‟distributed according to”. We then treat these i = 10 values as observations, and store them in a vector,
” means ‟distributed according to”. We then treat these i = 10 values as observations, and store them in a vector, 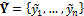 . We now use this vector of with
. We now use this vector of with 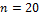 observations to determine the observed means by drawing ten different times a sample from a bivariate normal distribution
observations to determine the observed means by drawing ten different times a sample from a bivariate normal distribution
|
(15.01) |
where 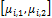 is the pair of parameter values created by DREAM and stored in vector x, and
is the pair of parameter values created by DREAM and stored in vector x, and 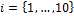 . The values of
. The values of 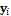 are stored in the vector,
are stored in the vector, 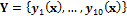 . The distance between the observed and simulated observations is not defined with a formal likelihood function, but rather with a distance function,
. The distance between the observed and simulated observations is not defined with a formal likelihood function, but rather with a distance function, 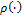 as follows (Turner and Sederberg, 1980)
as follows (Turner and Sederberg, 1980)
|
(15.02) |
The proposal is considered to be behavioral (= posterior solution) if the value of the distance function is smaller than 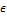 , a small positive value. We approximate the posterior distribution of the ten means in DREAM using N = 20 different chains and the distance function of Equation (15.02). The initial state of each chain is sampled randomly from
, a small positive value. We approximate the posterior distribution of the ten means in DREAM using N = 20 different chains and the distance function of Equation (15.02). The initial state of each chain is sampled randomly from 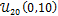 and standard values are used of the algorithmic variables (default
and standard values are used of the algorithmic variables (default 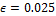 ).
).
Implementation of plugin functions
The complete source code can be found in DREAM SDK - Examples\D3\Drm_Example15\Plugin\Src_Cpp