Example 14

Case-Study XIV: Approximate Bayesian inference for hydrologic watershed model

The fourteenth case study illustrates the ability of DREAM for diagnostic model evaluation. A rather parsimonious 7-parameter lumped watershed model (also known as hmodel) is used with historical data from the French Broad River at Asheville, North Carolina. This is the driest of the 12 MOPEX basins described in the study of Duan et al. (2006). The model is illustrated schematically in Figure 14.01. The model transforms rainfall into runoff at the watershed outlet using explicit process descriptions of interception, throughfall, evaporation, runoff generation, percolation, and surface and subsurface routing.

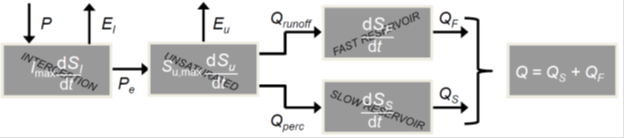
Figure 14.01. Schematic representation of the hmodel conceptual watershed

Daily discharge, mean areal precipitation, and mean areal potential evapotranspiration were derived from Duan et al. (2006) and used for diagnostic model evaluation with DREAM. Details about the basin and experimental data, and likelihood function can be found there, and will not be discussed herein. The same model was used in case study six to illustrate the generalized likelihood function.

Four different summary metrics of the discharge data are used for diagnostic inference with DREAM (activated with likelihood function 22), including S1 (-), the annual runoff coefficient, S2 (-) the annual baseflow coefficient, and S3 (day/mm) and S4 (-) two coefficients of the flow duration curve. The four different summary metrics are stored in the vector 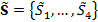. . A detailed description of these summary metrics can be found in Sadegh and Vrugt (2013) and interested readers are referred to this publication. The seven different parameter values of the hmodel and their prior uncertainty ranges are listed in Table 6.01.

Each time the hmodel is executed with the seven different parameter values stored in the vector x the simulated values of the summary metrics are computed from the modeled discharge record and stored in the vector 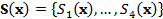. The following distance function, is used in DREAM to help determine whether we should accept the vector of proposed parameter values or not

where |·| denotes the modulus operator (absolute value). If this distance function is smaller than the small positive threshold ϵ the proposed parameter values are considered to be a sample of the posterior distribution. The initial population is drawn from the parameter ranges listed in Table 6.01 using Latin hypercube sampling. The posterior target distribution is sampled with DREAM using N = 10 different chains using standard settings for the algorithmic variables (default ϵ=0.025).

Implementation of plugin functions

The complete source code can be found in DREAM SDK - Examples\D3\Drm_Example14\Plugin\Src_Cpp