Case-Study VIII: Approximate Bayesian Computation of mixture distribution
This case study illustrates the ability of DREAM to perform statistical inference involving the use of summary metrics. This functionality, also known as Approximate Bayesian Computation (ABC) has been implemented in DREAM and the underlying theory and concepts have been published by Sadegh and Vrugt (2014). The ABC approach is particularly useful for diagnostic model evaluation as it relaxes the need for an explicit likelihood function in favor of one or multiple different summary statistics rooted in the relevant theory that together have a clearer and more compelling diagnostic power than some average (likelihood)-measure of the size of the error residuals. Vrugt and Sadegh (2013) have shown that this diagnostics approach enhances considerably our chances to diagnose and detect model structural errors. Indeed, the use of behavioral signatures helps to analyze and pinpoint which part of the model is malfunctioning and in need of further improvement.
This eight case study benchmarks the implementation of the ABC method against a simple mixture of two univariate normal distributions, 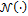
|
(8.01) |
where 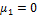 and
and 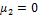 denote the mean of the first and second normal pdf of the mixture distribution, and
denote the mean of the first and second normal pdf of the mixture distribution, and 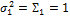 and
and 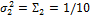 define their corresponding variances, respectively. The probability density function of
define their corresponding variances, respectively. The probability density function of 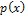 in Equation (2.01) is given by the following weighted sum of two normal densities
in Equation (2.01) is given by the following weighted sum of two normal densities
|
(8.02) |
This Equation is easy to derive if you follow the steps in case study III. Indeed, the determinant of 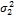 and
and 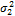 is simply equivalent to 1 and 1/10 respectively, and
is simply equivalent to 1 and 1/10 respectively, and 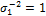 and
and 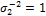 00.
00.
We can easily generate samples from this target distribution with DREAM if we evaluate directly the density of Equation (2.02). Instead, we follow a different procedure herein and use the ABC procedure in DREAM. This requires the user to define signatures of system behavior, which in the present context is equivalent to a summary metric of Equation (2.02). This summary metric, 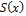 , is defined as follows
, is defined as follows
|
(8.03) |
where 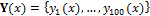 is a vector with hundred elements and |·| denotes the modulus operator (absolute value). The values of the
is a vector with hundred elements and |·| denotes the modulus operator (absolute value). The values of the 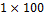 vector Y are drawn randomly from
vector Y are drawn randomly from 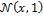 the univariate normal distribution with zero mean and unit standard deviation, thus
the univariate normal distribution with zero mean and unit standard deviation, thus 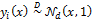 ,
, 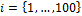 . The tilde symbol ‟
. The tilde symbol ‟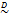 ” means ‟distributed according to".
” means ‟distributed according to".
The following distance function, 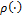 is used in DREAM to help determine whether we should accept the value of the parameter, x or not
is used in DREAM to help determine whether we should accept the value of the parameter, x or not
|
(8.04) |
The variable 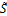 in Equation (8.04) denotes the observed value of the summary metric. This value is equal to zero in the present study. If the value of the distance function is smaller than some small nominal value
in Equation (8.04) denotes the observed value of the summary metric. This value is equal to zero in the present study. If the value of the distance function is smaller than some small nominal value 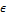 then
then 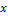 is accepted, and otherwise the proposed parameter value is rejected. The initial population is drawn from the univariate uniform distribution
is accepted, and otherwise the proposed parameter value is rejected. The initial population is drawn from the univariate uniform distribution 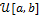 with
with 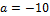 and
and 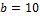 using Latin hypercube sampling. A total of N = 8 chains are created with DREAM using standard settings for the algorithmic variables.
using Latin hypercube sampling. A total of N = 8 chains are created with DREAM using standard settings for the algorithmic variables.
Implementation of plugin functions
The complete source code can be found in DREAM SDK - Examples\D3\Drm_Example08\Plugin\Src_Cpp