Example 10

Case-Study X: d-dimensional multimodal mixture distribution with multiplicative prior

According to Bayes law, the posterior density is equal to the product of the prior distribution and the likelihood function or, p(x) = pr(x) × L(x). In the previous case studies we have assumed that the prior distribution,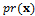, is multivariate uniform, and thus

The value of this constant is thus fixed and independent of the model parameter values used. With the use of such noninformative (flat) prior, the posterior density, 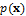, is simply proportional to the value of the likelihood function, 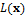and thus, 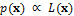. The value of 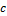in Equation (10.01) is easily derived if a uniform prior is used. Certainly, we know that any prior distribution must integrate to unity – a requirement for a proper probability distribution. If we apply this principle to the uniform prior distribution of the hmodel parameters of Table 9.01 we can write

We also know that the uniform distribution produces the same density for each feasible solution within its domain. Thus, the value of the constant 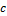is easily derived from the listed ranges of the hmodel parameters. This gives

If we thus take into explicit consideration the effect of the prior distribution on the posterior density in the previous case study we should write

Indeed, we can now use an equality sign rather than a proportionality sign. Nevertheless, this scaling factor of the posterior density has no effect on the parameter inference with DREAM. This changes however, if we use an informative prior distribution – that is – a distribution that is not flat but rather depends on the actual values of the parameters. Indeed, in case study XII we have considered such example with soil hydraulic parameters that were assumed to each have a Gaussian marginal prior distribution. Such distribution does not assign an equal prior density to the parameter values, but rather favors certain solutions over others – that is – parameter values that are close to the mean of the Gaussian prior will have a higher density than those further removed from the center of this distribution. This will affect the inference with DREAM as parameter values that do not agree with prior information are discouraged.

To explicate the effects of a prior distribution on the results of DREAM we consider in this tenth case study, a simple multivariate normal prior distribution, 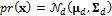with mean 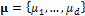and 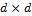covariance matrix 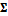. We assume that the mean of the prior distribution is equal to -2, and the covariance matrix is equivalent to Id, a 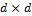matrix with values of one on the main diagonal and zero elsewhere, and thus 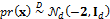. The tilde symbol ‟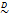” means ‟distributed according to".

We consider as likelihood function a mixture of two normal distributions

where the mean of the first and second component of the Gaussian mixture is equal to -5 and 5, respectively, and the covariance matrix equal to the identity matrix, Id. Now we can calculate the posterior density, 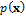as product of the prior, 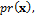and likelihood, 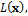using Bayes law

The initial population is drawn randomly from 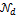(0,Id), the multivariate normal distribution with zero mean and covariance matrix equal to the identity matrix. We use N = 10 different chains with DREAM and apply default settings of the algorithmic variables.

Thus this case study does not use a uniform prior distribution for the parameters, but rather assumes an informative prior distribution. Such prior allows users to take into explicit consideration in the present study, parameter estimates or distributions derived from previous data and/or analysis.

Implementation of plugin functions

The complete source code can be found in DREAM SDK - Examples\D3\Drm_Example10\Plugin\Src_Cpp