Case-Study I: d-dimensional banana shaped Gaussian distribution

The first case study considers a d=10-dimensional twisted Gaussian probability density function which is given by the following unnormalized density (hence the proportionality sign)

where 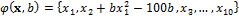is a function that is used to the multivariate normal to a twisted (banana-shaped) distribution. Here, 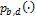signifies the probability density function of a multivariate normal distribution, 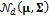, and thus 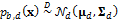, where the 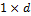vector 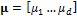stores the mean of the distribution, and the 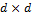matrix 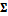signifies the variance-covariance matrix. The tilde symbol ‟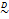” means ‟distributed according to”. The probability density function of 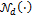is given by

where the symbol T denotes transpose, and |·| signifies the determinant operator, .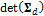

The mean of the normal distribution, 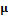was set to zero (all elements), and the covariance matrix is defined as a diagonal matrix, 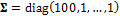. The entries of this matrix outside the main diagonal are all zero

and the value of b = 0.1. The initial sample was drawn from 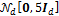, a normal distribution centered at zero and with covariance matrix equal to five times the identity matrix, 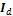, a 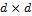(square) matrix with ones on the main diagonal and zeros elsewhere. We use N = 10 different chains with DREAM and apply default values of the algorithmic variables.

Implementation of plugin functions

The complete source code can be found in DREAM SDK - Examples\D1\Drm_D1_Example01\Plugin\Src_Cpp

///////////////////////////////////////////////////////////////////////////////////////////////////

// EvaluatorModel.cpp

///////////////////////////////////////////////////////////////////////////////////////////////////

//-------------------------------------------------------------------------------------------------

 HRESULT STDMETHODCALLTYPE CEvaluatorExample01::GetInputParams

//-------------------------------------------------------------------------------------------------

(

 IDreamInputParams* pIDreamInputParams // Pointer to DREAM input data to be defined

)

///////////////////////////////////////////////////////////////////////////////////////////////////

/*

 DESCRIPTION:

 The purpose of this function is to define default DREAM parameters for this particular project.

 This function is called by the main program to initialize data of each newly created simulation

 case. This data can be later modified in the GUI (except parameters locked by flag

 DreamSolver::disable_edit) or can be overwritten while reading case data from a file.

 In the AppTest console application, there is no GUI and this functions actually defines all

 input parameters that are subsequently used by DREAM Solver.

 RETURN VALUE:

 S_OK    - Operation successful

 S_FALSE - Function not implemented (program will continue)

 E_FAIL  - Operation failed (program will stop)

*/

///////////////////////////////////////////////////////////////////////////////////////////////////

{

 // Always check pIDreamInputParams pointer

 if(pIDreamInputParams == nullptr)

 {

   return E_INVALIDARG;

 }

 // Set default input parameters

 pIDreamInputParams->SetProblemDimension(2, DreamSolver::enable_edit);

 pIDreamInputParams->SetNumberOfMarkovChains(10, DreamSolver::enable_edit);

 pIDreamInputParams->SetNumberOfGenerations(25000, DreamSolver::enable_edit);

 pIDreamInputParams->SetLikelihoodChoice(eLikelihood::LIK_102, DreamSolver::disable_edit);

 pIDreamInputParams->SetInitialDistribution(eInitDistrib::eInitNormal, DreamSolver::enable_edit);

 pIDreamInputParams->SetOutlierTest(eOutlierTest::eOutlierIqr, DreamSolver::enable_edit);

 pIDreamInputParams->SetBoundHandling(eBoundHandling::eBoundUnbounded, DreamSolver::enable_edit);

 // Example can run in parallel mode (recommended mode)

 pIDreamInputParams->SetParallelMode(eParallelModeYes, DreamSolver::enable_edit);

 return S_OK;

}

//-------------------------------------------------------------------------------------------------

 HRESULT STDMETHODCALLTYPE CEvaluatorExample01::InitData

//-------------------------------------------------------------------------------------------------

(

 IDreamPluginInfo* pIPluginInfo            // Plugin information

, IDreamInputParViewer* pIDreamInputParams  // Current DREAM input parameters

)

///////////////////////////////////////////////////////////////////////////////////////////////////

/*

 DESCRIPTION:

 This function is called to prepare:

 A/ DREAM input data before accessing them via the IDreamDataSource interface and

 B/ all other local data required by evaluator for the calculation.  

 It can be also used to read needed data from a file in directory pIPluginInfo->m_strModelDataDir

 (directory ...Drm_ExampleXX\Model\Data).

         

 Remark 1: This function prepares DREAM input data in the evaluator according to current

 DREAM parameters defined by pIPluginInfo interface. Note that some parameters can be

 different from default parameters defined in function CEvaluatorExample::GetInputParams().

 Remark 2: This function should be called before using functions

 CEvaluatorExample::GetMinMaxData, ::GetNormalData, ::GetPriorData, ::GetPriorDataCustom,

 ::GetMeasurementData and ::GetBayesData. However, function CEvaluatorExample::GetInputParams()

 can be called independently.

 RETURN VALUE:

 S_OK    - Operation successful

 S_FALSE - Function not implemented (program will continue)

 E_FAIL  - Operation failed (program will stop)

*/

///////////////////////////////////////////////////////////////////////////////////////////////////

{

 // Check parameters

 if(pIPluginInfo == nullptr || pIDreamInputParams == nullptr)

 {

   // Invalid argument

   return E_INVALIDARG;

 }

 // Free memory from previous calculation

 FunctionsSC::DeleteMatrix(m_invC, m_invCSize);

 // Target covariance

 int iDim = m_invCSize = pIDreamInputParams->GetProblemDimension();

 double** C = nullptr;

 FunctionsSC::IdentityMatrix(C, iDim);

 C[0][0] = 100.0;

 FunctionsSC::CopyMatrix(m_invC, C, iDim);

 if(!FunctionsSC::Inv(m_invC, iDim))

 {

   return E_FAIL;

 }

 // Calculate integration constant

 double temp = pow(2.0 * pi<double>(), -(double)iDim / 2.0);

 double det = FunctionsSC::DeterminantLU(C, iDim);

 double temp2 = pow(det, -0.5);

 m_logF = log(temp * temp2);

 // log_F becomes - Inf for large d--> hence we set log_F to zero.

 // Also need to resolve this in importance distribution as well!!

 if(iDim > 150)

 {

   m_logF = 0.0;

 }

 m_b = 0.1;

 // Free allocated memory

 FunctionsSC::DeleteMatrix(C, iDim);

 return S_OK;

}

//-------------------------------------------------------------------------------------------------

 HRESULT STDMETHODCALLTYPE CEvaluatorExample01::GetNormalData

//-------------------------------------------------------------------------------------------------

(

 IDreamInputParViewer* pInputPar   // Interface to DREAM input parameters

, IDreamDataNormal* pINormalData    // Interface to normal distribution data

)

///////////////////////////////////////////////////////////////////////////////////////////////////

{

 // Always check pINormalData pointer

 if(pINormalData == nullptr)

 {

   return E_INVALIDARG;

 }

 // Fill mu data

 int iDim = pInputPar->GetProblemDimension();

 for(int iIndex = 0; iIndex < iDim; iIndex++)

 {

   pINormalData->AddMeanItem(0.0);

 }

 // Covariance matrix diagonal value

 pINormalData->SetCovarianceDiagonalValue(10.0);

 // Data added successfully

 return S_OK;

}

//-------------------------------------------------------------------------------------------------

 HRESULT STDMETHODCALLTYPE CEvaluatorExample01::EvaluateProposal

//-------------------------------------------------------------------------------------------------

(

 IDreamInputParViewer* pInputPar // Interface to DREAM input parameters

, int iSim              // input parameter (i-th simulation / Markov chain)

, IDreamMatrix* x       // input matrix (m_NumberOfMarkovChains x m_ProblemDimension)

, IDreamMatrix* res     // output matrix (Data_Dimension x m_NumberOfMarkovChains)

, BSTR strWorkingDir    // path to the current working directory (for current calculation thread)

, BSTR strModelDataDir  // path to the permanent directory with model data

, BSTR strModelBinDir   // path to the permanent directory with model executables

)

///////////////////////////////////////////////////////////////////////////////////////////////////

/*

 DESCRIPTION:

 The purpose of this function is to evaluate the current proposal (i.e. one single step

 of IDreamInputParams::GetNumberOfGenerations() steps) for iSim-th Markov chain. It computes

 the likelihood (or log-likelihood or the residual vector to be compared with the measurement

 - see the technical manual) for iSim-th row of input matrix "x" and returns the result

 in output matrix "res".  

 

 Parameter iSim is from interval <0, IDreamInputParams::GetNumberOfMarkovChains() - 1>.

 If pInputPar->GetVectorization() == eVectorization::eVectYes, then iSim = 0 and all proposals

 (for all Markov chains) should be evaluated in one step, i.e. during one call of this function.

 RETURN VALUE:

 S_OK    - Operation successful

 S_FALSE - Function not implemented (program will continue)

 E_FAIL  - Operation failed (program will stop)

*/

///////////////////////////////////////////////////////////////////////////////////////////////////

{

 // We should have m_invC initialized

 assert(m_invCSize != 0);

 // Temporary vector used for calculations

 double* tmpx = nullptr;

 FunctionsSC::CopyRowFromIDreamMatrix(iSim, tmpx, x);

 double logLtmp = 0.0;

 if(x->_colCount == 1) // 1-dimensional Gaussian

 {

   // 1-dimensional twisted Gaussian probability density function

   // logL = logF - 1/2 * invC * (x.^2)'

   // where:

   // x'  - transposition of "x"

   // .^2 - power of 2 of each element

   logLtmp = m_logF - 0.5 * m_invC[0][0] * tmpx[0] * tmpx[0];

 }

 else // N-dimensional Gaussian

 {

   // Introduce banana shaped nonlinearity between x(1) and x(2)

   // x(2) = x(2) + b * x(1)^2 - 100 * b

   tmpx[1] += m_b * tmpx[0] * tmpx[0] - 100.0 * m_b;

   // N-dimensional twisted Gaussian probability density function

   // logL = m_logF - 1/2 * sum(x'.*(invC * x'));  

   // where:

   // x'  - transposition of matrix "x"

   // sum - returns the sum of the elements of input along the first array dimension

   // .*  - multiplies arrays A and B element by element

   // vector1 = invC * x'

   double* vector1 = nullptr;

   FunctionsSC::MatrixColumnVectorProduct(vector1, m_invC, m_invCSize, m_invCSize,

                                          tmpx, x->_colCount);

   // vector2 = x'.*(invC * x') = vector1 .* vector2

   double* vector2 = nullptr;

   FunctionsSC::VectorVectorElementProduct(vector2, tmpx, x->_colCount, vector1, x->_colCount);

     

   // logL = m_logF - 1/2 * sum(x'.*(invC * x')) = m_logF - 0.5 sum(vector2)

   logLtmp = m_logF - 0.5 * FunctionsSC::VectorElementSum(vector2, x->_colCount);

   // Free allocated memory

   FunctionsSC::DeleteVector(vector1);

   FunctionsSC::DeleteVector(vector2);

 }

   

 // Replace content of res by tmp values

 res->_data[iSim] = logLtmp;

 // Free allocated memory

 FunctionsSC::DeleteVector(tmpx);

 return S_OK;

}